scgraph

SCGraph

PyPI version License: MIT PyPI Downloads

A Supply chain graph package for Python

scgraph

Quick Start:

Get the shortest maritime path length between Shanghai, China and Savannah, Georgia, USA

# Use a maritime network geograph
from scgraph.geographs.marnet import marnet_geograph
output = marnet_geograph.get_shortest_path(
    origin_node={"latitude": 31.23,"longitude": 121.47},
    destination_node={"latitude": 32.08,"longitude": -81.09},
    output_units='km',
)
print('Length: ',output['length']) #=> Length:  19596.4653

Documentation

How to Cite SCGraph in your Research

If you use SCGraph for your research, please consider citing the following paper:

Makowski, C., Saragih, A., Guter, W., Russell, T., Heinold, A., & Lekkakos, S. (2025). SCGraph: A dependency-free Python package for road, rail, and maritime shortest path routing generation and distance estimation. MIT Center for Transportation & Logistics Research Paper Series, (2025-028). https://ssrn.com/abstract=5388845

Or by using the BibTeX entry:

@article{makowski2025scgraph,
  title={SCGraph: A Dependency-Free Python Package for Road, Rail, and Maritime Shortest Path Routing Generation and Distance Estimation},
  author={Makowski, Connor and Saragih, Austin and Guter, Willem and Russell, Tim and Heinold, Arne and Lekkakos, Spyridon},
  journal={MIT Center for Transportation \& Logistics Research Paper Series},
  number={2025-028},
  year={2025},
  url={https://ssrn.com/abstract=5388845}
}

Getting Started

Installation

pip install scgraph

Basic Geograph Usage

Get the shortest path between two points on earth using a latitude / longitude pair.

In this case, calculate the shortest maritime path between Shanghai, China and Savannah, Georgia, USA.

# Use a maritime network geograph
from scgraph.geographs.marnet import marnet_geograph

# Note: The origin and destination nodes can be any latitude / longitude pair
output = marnet_geograph.get_shortest_path(
    origin_node={"latitude": 31.23,"longitude": 121.47},
    destination_node={"latitude": 32.08,"longitude": -81.09},
    output_units='km',
    # Optional: Cache the origin node's spanning tree for faster calculations on future calls from the same origin node when cache=True
    # Note: This will make the first call slower, but future calls using this origin node will be substantially faster.
    cache=True,
)
print('Length: ',output['length']) #=> Length:  19596.4653

Adding in a few additional parameters to the get_shortest_path function can change the output format as well as performance of the calculation.

# Use a maritime network geograph
from scgraph.geographs.marnet import marnet_geograph

# Get the shortest maritime path between Shanghai, China and Savannah, Georgia, USA
output = marnet_geograph.get_shortest_path(
    origin_node={"latitude": 31.23,"longitude": 121.47},
    destination_node={"latitude": 32.08,"longitude": -81.09},
    output_units='km',
    node_addition_lat_lon_bound=180, # Optional: The maximum distance in degrees to consider nodes when attempting to add the origin and destination nodes to the graph
    node_addition_type='quadrant', # Optional: Instead of connecting the origin node to the graph by the closest node, connect it to the closest node in each direction (NE, NW, SE, SW) if found within the node_addition_lat_lon_bound
    destination_node_addition_type='all', # Optional: Instead of connecting the destination node to the graph by the closest node, connect it to all nodes found within the node_addition_lat_lon_bound
    # When destination_node_addition_type='all' is set with a node_addition_lat_lon_bound=180, this will guarantee a solution can be found since the destination node will also connect to the origin node
)
print('Length: ',output['length']) #=> Length:  19596.4653

In the above example, the output variable is a dictionary with two keys: length and coordinate_path.

  • length: The distance between the passed origin and destination when traversing the graph along the shortest path
    • Notes:
      • This will be in the units specified by the output_units parameter.
      • output_units options:
        • km (kilometers - default)
        • m (meters)
        • mi (miles)
        • ft (feet)
  • coordinate_path: A list of lists [latitude,longitude] that make up the shortest path

You can also select a different algorithm function for the shortest_path:

from scgraph.geographs.marnet import marnet_geograph
from scgraph import Graph
output = marnet_geograph.get_shortest_path(
    origin_node={"latitude": 31.23,"longitude": 121.47},
    destination_node={"latitude": 32.08,"longitude": -81.09},
    # Optional: Specify an algorithm_fn to call when solving the shortest_path
    algorithm_fn=Graph.bmssp,
)

Don't neglect the very efficient distance matrix function to quickly get the distances between multiple points on the graph. Each origin graph entry point and spanning tree is cached so you can generate massive distance matricies incredibly quickly (approaching 50 nano seconds per distance for large enough distance matricies).

from scgraph.geographs.us_freeway import us_freeway_geograph

cities = [
    {"latitude": 34.0522, "longitude": -118.2437},  # Los Angeles
    {"latitude": 40.7128, "longitude": -74.0060},   # New York City
    {"latitude": 41.8781, "longitude": -87.6298},   # Chicago
    {"latitude": 29.7604, "longitude": -95.3698},   # Houston
]

distance_matrix = us_freeway_geograph.distance_matrix(cities, output_units='km')
# [
#  [0.0, 4510.965665644833, 3270.3864033755776, 2502.886438995942],
#  [4510.9656656448415, 0.0, 1288.473118634311, 2637.5821542546687],
#  [3270.3864033755744, 1288.4731186343113, 0.0, 1913.1928919854067],
#  [2502.886438995935, 2637.5821542546687, 1913.1928919854076, 0.0],
# ]

For more examples including viewing the output on a map, see the example notebook.

Examples with Google Colab

GridGraph usage

Example:

  • Create a grid of 20x20 cells.
    • This creates a grid based graph with connections to all 8 neighbors for each grid item.
    • Each grid item has 4 cardinal connections at length 1 and 4 diagonal connections at length sqrt(2)
  • Create a wall from (10,5) to (10,19).
    • This would foce any path to go to the bottom of the graph to get around the wall.
  • Get the shortest path between (2,10) and (18,10)
    • Note: The length of this path should be 16 without the wall and 20.9704 with the wall.
from scgraph import GridGraph

x_size = 20
y_size = 20
blocks = [(10, i) for i in range(5, y_size)]

# Create the GridGraph object
gridGraph = GridGraph(
    x_size=x_size,
    y_size=y_size,
    blocks=blocks,
    add_exterior_walls=True,
)

# Solve the shortest path between two points
output = gridGraph.get_shortest_path(
    origin_node={"x": 2, "y": 10},
    destination_node={"x": 18, "y": 10},
    # Optional: Specify the output coodinate format (default is 'list_of_dicts)
    output_coordinate_path="list_of_lists",
    # Optional: Cache the origin point spanning_tree for faster calculations on future calls
    cache=True,
)

print(output)
#=> {'length': 20.9704, 'coordinate_path': [[2, 10], [3, 9], [4, 8], [5, 8], [6, 7], [7, 6], [8, 5], [9, 4], [10, 4], [11, 4], [12, 5], [13, 6], [14, 7], [15, 7], [16, 8], [17, 9], [18, 10]]}

About

Key Features

  • Graph:
    • A low level graph object that has methods for validating graphs, calculating shortest paths, and more.
    • See: Graph Documentation
    • Contains the following methods:
      • validate_graph: Validates symmetry and connectedness of a graph.
      • dijkstra: Calculates the shortest path between two nodes using Dijkstra's algorithm.
      • dijkstra_makowski: Calculates the shortest path between two nodes using a modified version of Dijkstra's algorithm designed for real world performance
      • dijkstra_negative: Calculates the shortest path between two nodes using a modified version of Dijkstra's algorithm that supports negative edge weights and detects negative cycles.
      • a_star: Modified version of dijkstra_makowski that incorporates a heuristic function to guide the search.
      • bellman_ford: Calculates the shortest path between two nodes using the Bellman-Ford algorithm.
      • bmssp: Calculates the shortest path between two nodes using a modified version of the BMSSP Algorithm. See the BmsspSolver.
  • GeoGraphs:
    • A geographic graph data structure that allows for the calculation of shortest paths between two points on earth
    • Uses latitude / longitude pairs to represent points on earth
    • Supports maritime, rail, road and other geographic networks
    • Uses a sparse network data structure to represent the graph
    • How to use it - Calculate the shortest path between two points on earth
      • Inputs:
        • A latitude / longitude pair for the origin
        • A latitude / longitude pair for the destination
      • Calculation:
        • See the Graph documentation above for available algorithms.
      • Returns:
        • path:
          • A list of lists [latitude, longitude] that make up the shortest path
        • length:
          • The distance (in the units requested) between the two points
    • Precompiled Geographs offer Antimeridian support
    • Arbitrary start and end points are supported
      • Start and end points do not need to be in the graph
    • Cached shortest path calculations can be used for very fast repetative calculations from the same origin node in a GeoGraph.
      • This is done by caching the origin node's spanning tree
      • The first call will be slower, but future calls using this origin node will be substantially faster.
  • GridGraphs:
    • A grid based graph data structure that allows for the calculation of shortest paths between two points on a grid
    • See: GridGraph Documentation
    • Supports arbitrary grid sizes and blockages
    • Uses a sparse network data structure to represent the graph
    • How to use it - Calculate the shortest path between two points on a grid
      • Inputs:
        • A (x,y) coordinate on the grid for the origin
        • A (x,y) coordinate on the grid for the destination
      • Calculation:
        • Algorithms:
          • Dijkstra's algorithm
          • Modified Dijkstra algorithm
          • A* algorithm (Extension of the Modified Dijkstra)
      • Returns:
        • length:
          • The distance between the two points on the grid
        • coordinate_path:
          • A list of dicts {"x": x, "y": y} representing the path taken through the grid
    • Arbitrary start and end points are supported
      • Start and end points do not need to be in the graph
    • Arbitrary connection matricies are supported
      • Cardinal connections (up, down, left, right) and diagonal connections (up-left, up-right, down-left, down-right) are used by default
      • Custom connection matricies can be used to change the connections between grid items
    • Cached shortest path calculations can be used for very fast repetative calculations to or from the same point in a GridGraph.
  • Other Useful Features:

Included GeoGraphs

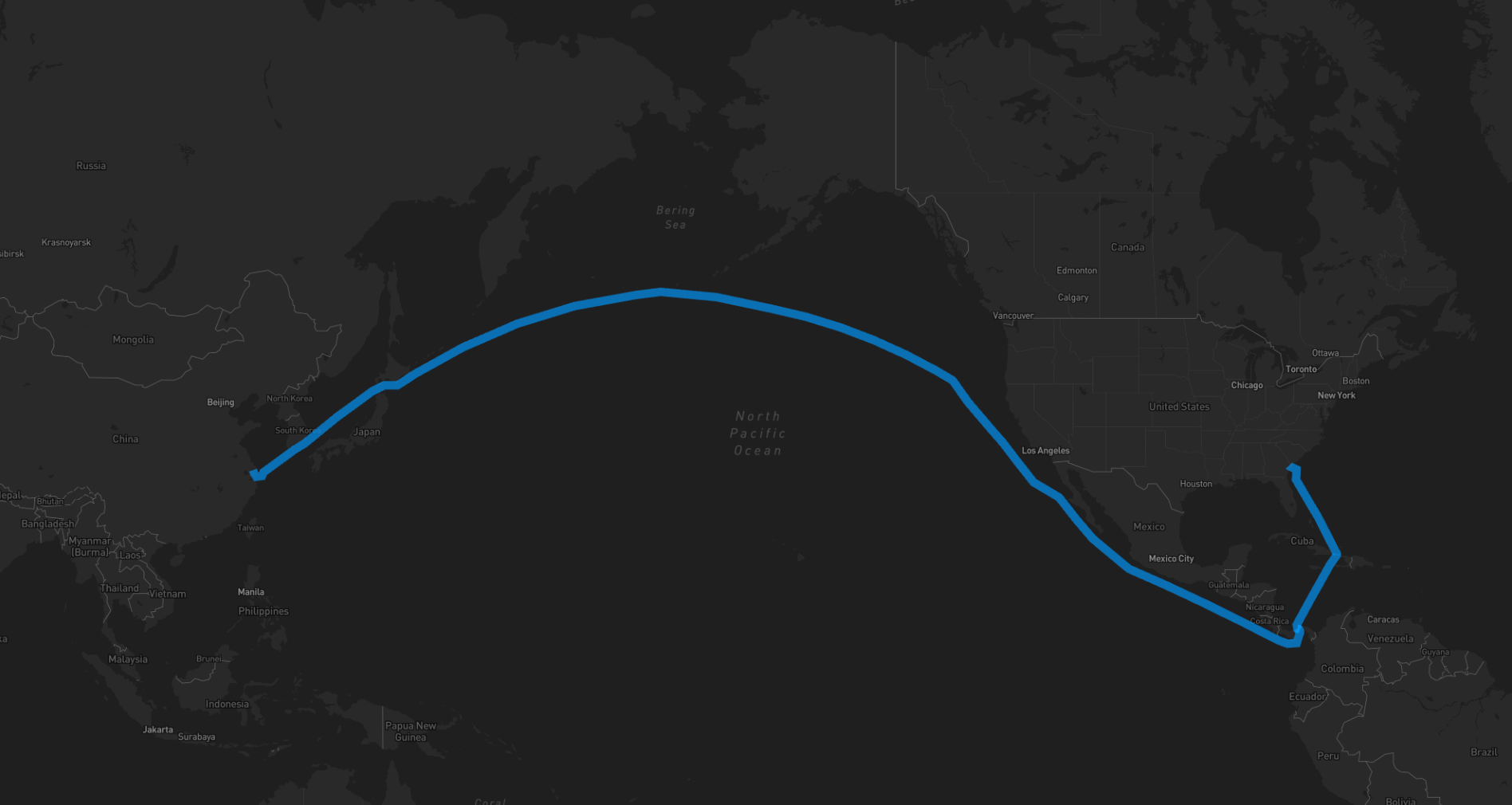
  • marnet_geograph:
    • What: A maritime network data set from searoute
    • Use: from scgraph.geographs.marnet import marnet_geograph
    • Attribution: searoute
    • Length Measurement: Kilometers
    • Marnet Picture
  • oak_ridge_maritime_geograph:
  • north_america_rail_geograph:
  • us_freeway_geograph:
  • scgraph_data geographs:
    • What: Additional geographs are available in the scgraph_data package
      • Note: These include larger geographs like the world highways geograph and world railways geograph.
    • Installation: pip install scgraph_data
    • Use: from scgraph_data.world_highways import world_highways_geograph
    • See: scgraph_data for more information and all available geographs.
  • Custom Geographs:

Advanced Usage

Using scgraph_data geographs

Using scgraph_data geographs:

  • Note: Make sure to install the scgraph_data package before using these geographs
from scgraph_data.world_railways import world_railways_geograph
from scgraph import Graph

# Get the shortest path between Kalamazoo Michigan and Detroit Michigan by Train
output = world_railways_geograph.get_shortest_path(
    origin_node={"latitude": 42.29,"longitude": -85.58},
    destination_node={"latitude": 42.33,"longitude": -83.05},
    # Optional: Use the A* algorithm
    algorithm_fn=Graph.a_star,
    # Optional: Pass the haversine function as the heuristic function to the A* algorithm
    algorithm_kwargs={"heuristic_fn": world_railways_geograph.haversine},
)

Building your own Geographs from Open Source Data

You can build your own geographs using various tools and data sources. For example, you can use OpenStreetMap data to create a high fidelity geograph for a specific area.

Follow this step by step guide on how to create a geograph from OpenStreetMap data. For this example, we will use some various tools to create a geograph for highways (including seconday highways) in Michigan, USA.

Download an OSM PBF file using the AWS CLI:

  • Geofabrik is a good source for smaller OSM PBF files. See: https://download.geofabrik.de/
  • To keep things generalizable, you can also download the entire planet OSM PBF file using AWS. But you should consider downloading a smaller region if you are only interested in a specific area.
    • Note: For this, you will need to install the AWS CLI.
    • Note: The planet OSM PBF file is very large (About 100GB)
    
aws s3 cp s3://osm-pds/planet-latest.osm.pbf .

  • Use Osmium to filter and extract the highways from the OSM PBF file.

    • Install osmium on macOS:

      brew install osmium-tool

    • Install osmium on Ubuntu:

      sudo apt-get install osmium-tool

  • Download a Poly file for the area you are interested in. This is a polygon file that defines the area you want to extract from the OSM PBF file.

    • For Michigan, you can download the poly file from Geofabrik:

      curl https://download.geofabrik.de/north-america/us/michigan.poly > michigan.poly

    • Google around to find an appropriate poly file for your area of interest.

  • Filter and extract as GeoJSON (EG: Michigan) substituting the poly and pbf file names as needed:

    osmium extract -p michigan.poly --overwrite -o michigan.osm.pbf planet-latest.osm.pbf

  • Filter the OSM PBF file to only areas of interest and export to GeoJSON:

    osmium tags-filter michigan.osm.pbf w/highway=motorway,trunk,primary,motorway_link,trunk_link,primary_link,secondary,secondary_link,tertiary,tertiary_link -t --overwrite -o michigan_roads.osm.pbf
osmium export michigan_roads.osm.pbf -f geojson --overwrite -o michigan_roads.geojson

  • Simplify the geojson

    • This uses some tools in the SCGraph library as well as Mapshaper to simplify the geojson files.
    • Mapshaper is a CLI and web tool for simplifying and editing geojson files.

    • To install Mapshaper for CLI use, use NPM:

      npm install -g mapshaper

    • Mapshaper is particularly helpful since it repairs intersections in the lines which is crutial for geographs to work properly.

    • Mapshaper, however, does not handle larger files very well, so it is recommended to simplify the geojson file first using the scgraph.helpers.geojson.simplify_geojson function first to reduce the size of the file.
    • Make sure to tailor the parameters to your needs.
    python -c "from scgraph.helpers.geojson import simplify_geojson; simplify_geojson('michigan_roads.geojson', 'michigan_roads_simple.geojson', precision=4, pct_to_keep=100, min_points=3, silent=False)"
mapshaper michigan_roads_simple.geojson -simplify 10% -filter-fields -o force michigan_roads_simple.geojson
mapshaper michigan_roads_simple.geojson -snap -clean -o force michigan_roads_simple.geojson

  • Load the newly created geojson file as a geograph:

    • Note: The GeoGraph.load_from_geojson function is used to load the geojson file as a geograph.
    • This will create a geograph that can be used to calculate shortest paths between points on the graph.
    from scgraph import GeoGraph
michigan_roads_geograph = GeoGraph.load_from_geojson('michigan_roads_simple.geojson')

Custom Graphs and Geographs

Modify an existing geograph: See the notebook here

You can specify your own custom graphs for direct access to the solving algorithms. This requires the use of the low level Graph class

from scgraph import Graph

# Define an arbitrary graph
# See the graph definitions here:
# https://connor-makowski.github.io/scgraph/scgraph/graph.html#Graph.validate_graph
graph = [
    {1: 5, 2: 1},
    {0: 5, 2: 2, 3: 1},
    {0: 1, 1: 2, 3: 4, 4: 8},
    {1: 1, 2: 4, 4: 3, 5: 6},
    {2: 8, 3: 3},
    {3: 6}
]

# Optional: Validate your graph
Graph.validate_graph(graph=graph)

# Get the shortest path between idx 0 and idx 5
output = Graph.dijkstra_makowski(graph=graph, origin_id=0, destination_id=5)
#=> {'path': [0, 2, 1, 3, 5], 'length': 10}

You can also use a slightly higher level GeoGraph class to work with latitude / longitude pairs

from scgraph import GeoGraph

# Define nodes
# See the nodes definitions here:
# https://connor-makowski.github.io/scgraph/scgraph/geograph.html#GeoGraph.__init__
nodes = [
    # London
    [51.5074, -0.1278],
    # Paris
    [48.8566, 2.3522],
    # Berlin
    [52.5200, 13.4050],
    # Rome
    [41.9028, 12.4964],
    # Madrid
    [40.4168, -3.7038],
    # Lisbon
    [38.7223, -9.1393]
]
# Define a graph
# See the graph definitions here:
# https://connor-makowski.github.io/scgraph/scgraph/graph.html#Graph.validate_graph
graph = [
    # From London
    {
        # To Paris
        1: 311,
    },
    # From Paris
    {
        # To London
        0: 311,
        # To Berlin
        2: 878,
        # To Rome
        3: 1439,
        # To Madrid
        4: 1053
    },
    # From Berlin
    {
        # To Paris
        1: 878,
        # To Rome
        3: 1181,
    },
    # From Rome
    {
        # To Paris
        1: 1439,
        # To Berlin
        2: 1181,
    },
    # From Madrid
    {
        # To Paris
        1: 1053,
        # To Lisbon
        5: 623
    },
    # From Lisbon
    {
        # To Madrid
        4: 623
    }
]

# Create a GeoGraph object
my_geograph = GeoGraph(nodes=nodes, graph=graph)

# Optional: Validate your graph
my_geograph.validate_graph()

# Optional: Validate your nodes
my_geograph.validate_nodes()

# Get the shortest path between two points
# In this case, Birmingham England and Zaragoza Spain
# Since Birmingham and Zaragoza are not in the graph,
# the algorithm will add them into the graph.
# See: https://connor-makowski.github.io/scgraph/scgraph/geograph.html#GeoGraph.get_shortest_path
# Expected output would be to go from
# Birmingham -> London -> Paris -> Madrid -> Zaragoza

output = my_geograph.get_shortest_path(
    # Birmingham England
    origin_node = {'latitude': 52.4862, 'longitude': -1.8904},
    # Zaragoza Spain
    destination_node = {'latitude': 41.6488, 'longitude': -0.8891}
)
print(output)
# {
#     'length': 1799.4323,
#     'coordinate_path': [
#         [52.4862, -1.8904],
#         [51.5074, -0.1278],
#         [48.8566, 2.3522],
#         [40.4168, -3.7038],
#         [41.6488, -0.8891]
#     ]
# }

Development

Running Tests, Prettifying Code, and Updating Docs

Make sure Docker is installed and running on a Unix system (Linux, MacOS, WSL2).

  • Create a docker container and drop into a shell
    • ./run.sh
  • Run all tests (see ./utils/test.sh)
    • ./run.sh test
  • Prettify the code (see ./utils/prettify.sh)
    • ./run.sh prettify

  • Update the docs (see ./utils/docs.sh)

    • ./run.sh docs

  • Note: You can and should modify the Dockerfile to test different python versions.

Attributions and Thanks

Originally inspired by searoute including the use of one of their datasets that has been modified to work properly with this package.

  1"""
  2# SCGraph
  3[![PyPI version](https://badge.fury.io/py/scgraph.svg)](https://badge.fury.io/py/scgraph)
  4[![License: MIT](https://img.shields.io/badge/License-MIT-yellow.svg)](https://opensource.org/licenses/MIT)
  5[![PyPI Downloads](https://img.shields.io/pypi/dm/scgraph.svg?label=PyPI%20downloads)](https://pypi.org/project/scgraph/)
  6<!-- [![PyPI Downloads](https://pepy.tech/badge/scgraph)](https://pypi.org/project/scgraph/) -->
  7
  8
  9### A Supply chain graph package for Python
 10
 11
 12![scgraph](https://raw.githubusercontent.com/connor-makowski/scgraph/main/static/scgraph.png)
 13
 14## Quick Start:
 15Get the shortest maritime path length between Shanghai, China and Savannah, Georgia, USA
 16```py
 17# Use a maritime network geograph
 18from scgraph.geographs.marnet import marnet_geograph
 19output = marnet_geograph.get_shortest_path(
 20    origin_node={"latitude": 31.23,"longitude": 121.47},
 21    destination_node={"latitude": 32.08,"longitude": -81.09},
 22    output_units='km',
 23)
 24print('Length: ',output['length']) #=> Length:  19596.4653
 25```
 26
 27### Documentation
 28
 29- Docs: https://connor-makowski.github.io/scgraph/scgraph.html
 30- Git Repo: https://github.com/connor-makowski/scgraph
 31- Paper: https://ssrn.com/abstract=5388845
 32
 33### How to Cite SCGraph in your Research
 34
 35If you use SCGraph for your research, please consider citing the following paper:
 36
 37> Makowski, C., Saragih, A., Guter, W., Russell, T., Heinold, A., & Lekkakos, S. (2025). SCGraph: A dependency-free Python package for road, rail, and maritime shortest path routing generation and distance estimation. MIT Center for Transportation & Logistics Research Paper Series, (2025-028). https://ssrn.com/abstract=5388845
 38
 39Or by using the BibTeX entry:
 40
 41```
 42@article{makowski2025scgraph,
 43  title={SCGraph: A Dependency-Free Python Package for Road, Rail, and Maritime Shortest Path Routing Generation and Distance Estimation},
 44  author={Makowski, Connor and Saragih, Austin and Guter, Willem and Russell, Tim and Heinold, Arne and Lekkakos, Spyridon},
 45  journal={MIT Center for Transportation \& Logistics Research Paper Series},
 46  number={2025-028},
 47  year={2025},
 48  url={https://ssrn.com/abstract=5388845}
 49}
 50```
 51
 52# Getting Started
 53
 54## Installation
 55
 56```
 57pip install scgraph
 58```
 59
 60## Basic Geograph Usage
 61
 62Get the shortest path between two points on earth using a latitude / longitude pair.
 63
 64In this case, calculate the shortest maritime path between Shanghai, China and Savannah, Georgia, USA.
 65
 66```py
 67# Use a maritime network geograph
 68from scgraph.geographs.marnet import marnet_geograph
 69
 70# Note: The origin and destination nodes can be any latitude / longitude pair
 71output = marnet_geograph.get_shortest_path(
 72    origin_node={"latitude": 31.23,"longitude": 121.47},
 73    destination_node={"latitude": 32.08,"longitude": -81.09},
 74    output_units='km',
 75    # Optional: Cache the origin node's spanning tree for faster calculations on future calls from the same origin node when cache=True
 76    # Note: This will make the first call slower, but future calls using this origin node will be substantially faster.
 77    cache=True,
 78)
 79print('Length: ',output['length']) #=> Length:  19596.4653
 80```
 81
 82Adding in a few additional parameters to the `get_shortest_path` function can change the output format as well as performance of the calculation.
 83```py
 84# Use a maritime network geograph
 85from scgraph.geographs.marnet import marnet_geograph
 86
 87# Get the shortest maritime path between Shanghai, China and Savannah, Georgia, USA
 88output = marnet_geograph.get_shortest_path(
 89    origin_node={"latitude": 31.23,"longitude": 121.47},
 90    destination_node={"latitude": 32.08,"longitude": -81.09},
 91    output_units='km',
 92    node_addition_lat_lon_bound=180, # Optional: The maximum distance in degrees to consider nodes when attempting to add the origin and destination nodes to the graph
 93    node_addition_type='quadrant', # Optional: Instead of connecting the origin node to the graph by the closest node, connect it to the closest node in each direction (NE, NW, SE, SW) if found within the node_addition_lat_lon_bound
 94    destination_node_addition_type='all', # Optional: Instead of connecting the destination node to the graph by the closest node, connect it to all nodes found within the node_addition_lat_lon_bound
 95    # When destination_node_addition_type='all' is set with a node_addition_lat_lon_bound=180, this will guarantee a solution can be found since the destination node will also connect to the origin node
 96)
 97print('Length: ',output['length']) #=> Length:  19596.4653
 98```
 99
100In the above example, the `output` variable is a dictionary with two keys: `length` and `coordinate_path`.
101
102- `length`: The distance between the passed origin and destination when traversing the graph along the shortest path
103    - Notes:
104        - This will be in the units specified by the `output_units` parameter.
105        - `output_units` options:
106            - `km` (kilometers - default)
107            - `m` (meters)
108            - `mi` (miles)
109            - `ft` (feet)
110- `coordinate_path`: A list of lists [`latitude`,`longitude`] that make up the shortest path
111
112
113You can also select a different algorithm function for the shortest_path:
114```py
115from scgraph.geographs.marnet import marnet_geograph
116from scgraph import Graph
117output = marnet_geograph.get_shortest_path(
118    origin_node={"latitude": 31.23,"longitude": 121.47},
119    destination_node={"latitude": 32.08,"longitude": -81.09},
120    # Optional: Specify an algorithm_fn to call when solving the shortest_path
121    algorithm_fn=Graph.bmssp,
122)
123```
124
125Don't neglect the very efficient distance matrix function to quickly get the distances between multiple points on the graph. Each origin graph entry point and spanning tree is cached so you can generate massive distance matricies incredibly quickly (approaching 50 nano seconds per distance for large enough distance matricies).
126```py
127from scgraph.geographs.us_freeway import us_freeway_geograph
128
129cities = [
130    {"latitude": 34.0522, "longitude": -118.2437},  # Los Angeles
131    {"latitude": 40.7128, "longitude": -74.0060},   # New York City
132    {"latitude": 41.8781, "longitude": -87.6298},   # Chicago
133    {"latitude": 29.7604, "longitude": -95.3698},   # Houston
134]
135
136distance_matrix = us_freeway_geograph.distance_matrix(cities, output_units='km')
137# [
138#  [0.0, 4510.965665644833, 3270.3864033755776, 2502.886438995942],
139#  [4510.9656656448415, 0.0, 1288.473118634311, 2637.5821542546687],
140#  [3270.3864033755744, 1288.4731186343113, 0.0, 1913.1928919854067],
141#  [2502.886438995935, 2637.5821542546687, 1913.1928919854076, 0.0],
142# ]
143```
144
145For more examples including viewing the output on a map, see the [example notebook](https://colab.research.google.com/github/connor-makowski/scgraph/blob/main/examples/getting_started.ipynb).
146
147
148### Examples with Google Colab
149
150- [Getting Started](https://colab.research.google.com/github/connor-makowski/scgraph/blob/main/examples/getting_started.ipynb)
151- [Creating A Multi Path Geojson](https://colab.research.google.com/github/connor-makowski/scgraph/blob/main/examples/multi_path_geojson.ipynb)
152- [Modifying A Geograph](https://colab.research.google.com/github/connor-makowski/scgraph/blob/main/examples/geograph_modifications.ipynb)
153
154## GridGraph usage
155
156Example:
157- Create a grid of 20x20 cells.
158    - This creates a grid based graph with connections to all 8 neighbors for each grid item.
159    - Each grid item has 4 cardinal connections at length 1 and 4 diagonal connections at length sqrt(2)
160- Create a wall from (10,5) to (10,19).
161    - This would foce any path to go to the bottom of the graph to get around the wall.
162- Get the shortest path between (2,10) and (18,10)
163    - Note: The length of this path should be 16 without the wall and 20.9704 with the wall.
164
165```py
166from scgraph import GridGraph
167
168x_size = 20
169y_size = 20
170blocks = [(10, i) for i in range(5, y_size)]
171
172# Create the GridGraph object
173gridGraph = GridGraph(
174    x_size=x_size,
175    y_size=y_size,
176    blocks=blocks,
177    add_exterior_walls=True,
178)
179
180# Solve the shortest path between two points
181output = gridGraph.get_shortest_path(
182    origin_node={"x": 2, "y": 10},
183    destination_node={"x": 18, "y": 10},
184    # Optional: Specify the output coodinate format (default is 'list_of_dicts)
185    output_coordinate_path="list_of_lists",
186    # Optional: Cache the origin point spanning_tree for faster calculations on future calls
187    cache=True,
188)
189
190print(output)
191#=> {'length': 20.9704, 'coordinate_path': [[2, 10], [3, 9], [4, 8], [5, 8], [6, 7], [7, 6], [8, 5], [9, 4], [10, 4], [11, 4], [12, 5], [13, 6], [14, 7], [15, 7], [16, 8], [17, 9], [18, 10]]}
192```
193
194
195# About
196## Key Features
197
198- `Graph`:
199    - A low level graph object that has methods for validating graphs, calculating shortest paths, and more.
200    - See: [Graph Documentation](https://connor-makowski.github.io/scgraph/scgraph/graph.html)
201    - Contains the following methods:
202        - `validate_graph`: Validates symmetry and connectedness of a graph.
203        - `dijkstra`: Calculates the shortest path between two nodes using Dijkstra's algorithm.
204        - `dijkstra_makowski`: Calculates the shortest path between two nodes using a modified version of Dijkstra's algorithm designed for real world performance
205        - `dijkstra_negative`: Calculates the shortest path between two nodes using a modified version of Dijkstra's algorithm that supports negative edge weights and detects negative cycles.
206        - `a_star`: Modified version of `dijkstra_makowski` that incorporates a heuristic function to guide the search.
207        - `bellman_ford`: Calculates the shortest path between two nodes using the Bellman-Ford algorithm.
208        - `bmssp`: Calculates the shortest path between two nodes using a modified version of the [BMSSP Algorithm](https://arxiv.org/pdf/2504.17033). See the [BmsspSolver](https://connor-makowski.github.io/scgraph/scgraph/bmssp.html).
209- `GeoGraph`s:
210    - A geographic graph data structure that allows for the calculation of shortest paths between two points on earth
211    - Uses latitude / longitude pairs to represent points on earth
212    - Supports maritime, rail, road and other geographic networks
213    - Uses a sparse network data structure to represent the graph
214    - How to use it - Calculate the shortest path between two points on earth
215        - Inputs:
216            - A latitude / longitude pair for the origin
217            - A latitude / longitude pair for the destination
218        - Calculation:
219            - See the `Graph` documentation above for available algorithms.
220        - Returns:
221            - `path`:
222                - A list of lists `[latitude, longitude]` that make up the shortest path
223            - `length`:
224                - The distance (in the units requested) between the two points
225    - Precompiled Geographs offer Antimeridian support
226    - Arbitrary start and end points are supported
227        - Start and end points do not need to be in the graph
228    - Cached shortest path calculations can be used for very fast repetative calculations from the same origin node in a GeoGraph.
229        - This is done by caching the origin node's spanning tree
230        - The first call will be slower, but future calls using this origin node will be substantially faster.
231- `GridGraph`s:
232    - A grid based graph data structure that allows for the calculation of shortest paths between two points on a grid
233    - See: [GridGraph Documentation](https://connor-makowski.github.io/scgraph/scgraph/grid.html)
234    - Supports arbitrary grid sizes and blockages
235    - Uses a sparse network data structure to represent the graph
236    - How to use it - Calculate the shortest path between two points on a grid
237        - Inputs:
238            - A (x,y) coordinate on the grid for the origin
239            - A (x,y) coordinate on the grid for the destination
240        - Calculation:
241            - Algorithms:
242                - Dijkstra's algorithm
243                - Modified Dijkstra algorithm
244                - A* algorithm (Extension of the Modified Dijkstra)
245        - Returns:
246            - `length`:
247                - The distance between the two points on the grid
248            - `coordinate_path`:
249                - A list of dicts `{"x": x, "y": y}` representing the path taken through the grid
250    - Arbitrary start and end points are supported
251        - Start and end points do not need to be in the graph
252    - Arbitrary connection matricies are supported
253        - Cardinal connections (up, down, left, right) and diagonal connections (up-left, up-right, down-left, down-right) are used by default
254        - Custom connection matricies can be used to change the connections between grid items
255    - Cached shortest path calculations can be used for very fast repetative calculations to or from the same point in a GridGraph.
256- Other Useful Features:
257    - `CacheGraph`s:
258        - A graph extension that caches spanning trees for fast shortest path calculations on repeat calls from the same origin node
259        - See: [CacheGraphs Documentation](https://connor-makowski.github.io/scgraph/scgraph/cache.html)
260    - `SpanningTree`s:
261        - See: [Spanning Trees Documentation](https://connor-makowski.github.io/scgraph/scgraph/spanning.html)
262
263## Included GeoGraphs
264
265- marnet_geograph:
266    - What: A maritime network data set from searoute
267    - Use: `from scgraph.geographs.marnet import marnet_geograph`
268    - Attribution: [searoute](https://github.com/genthalili/searoute-py)
269    - Length Measurement: Kilometers
270    - [Marnet Picture](https://raw.githubusercontent.com/connor-makowski/scgraph/main/static/marnet.png)
271- oak_ridge_maritime_geograph:
272    - What: A maritime data set from the Oak Ridge National Laboratory campus
273    - Use: `from scgraph.geographs.oak_ridge_maritime import oak_ridge_maritime_geograph`
274    - Attribution: [Oak Ridge National Laboratory](https://www.ornl.gov/) with data from [Geocommons](http://geocommons.com/datasets?id=25)
275    - Length Measurement: Kilometers
276    - [Oak Ridge Maritime Picture](https://raw.githubusercontent.com/connor-makowski/scgraph/main/static/oak_ridge_maritime.png)
277- north_america_rail_geograph:
278    - What: Class 1 Rail network for North America
279    - Use: `from scgraph.geographs.north_america_rail import north_america_rail_geograph`
280    - Attribution: [U.S. Department of Transportation: ArcGIS Online](https://geodata.bts.gov/datasets/usdot::north-american-rail-network-lines-class-i-freight-railroads-view/about)
281    - Length Measurement: Kilometers
282    - [North America Rail Picture](https://raw.githubusercontent.com/connor-makowski/scgraph/main/static/north_america_rail.png)
283- us_freeway_geograph:
284    - What: Freeway network for the United States
285    - Use: `from scgraph.geographs.us_freeway import us_freeway_geograph`
286    - Attribution: [U.S. Department of Transportation: ArcGIS Online](https://hub.arcgis.com/datasets/esri::usa-freeway-system-over-1500k/about)
287    - Length Measurement: Kilometers
288    - [US Freeway Picture](https://raw.githubusercontent.com/connor-makowski/scgraph/main/static/us_freeway.png)
289- `scgraph_data` geographs:
290    - What: Additional geographs are available in the `scgraph_data` package
291        - Note: These include larger geographs like the world highways geograph and world railways geograph.
292    - Installation: `pip install scgraph_data`
293    - Use: `from scgraph_data.world_highways import world_highways_geograph`
294    - See: [scgraph_data](https://github.com/connor-makowski/scgraph_data) for more information and all available geographs.
295- Custom Geographs:
296    - What: Users can create their own geographs from various data sources
297    - See: [Building your own Geographs from Open Source Data](https://github.com/connor-makowski/scgraph#building-your-own-geographs-from-open-source-data)
298
299# Advanced Usage
300
301## Using scgraph_data geographs
302
303Using `scgraph_data` geographs:
304- Note: Make sure to install the `scgraph_data` package before using these geographs
305```py
306from scgraph_data.world_railways import world_railways_geograph
307from scgraph import Graph
308
309# Get the shortest path between Kalamazoo Michigan and Detroit Michigan by Train
310output = world_railways_geograph.get_shortest_path(
311    origin_node={"latitude": 42.29,"longitude": -85.58},
312    destination_node={"latitude": 42.33,"longitude": -83.05},
313    # Optional: Use the A* algorithm
314    algorithm_fn=Graph.a_star,
315    # Optional: Pass the haversine function as the heuristic function to the A* algorithm
316    algorithm_kwargs={"heuristic_fn": world_railways_geograph.haversine},
317)
318```
319
320## Building your own Geographs from Open Source Data
321You can build your own geographs using various tools and data sources. For example, you can use OpenStreetMap data to create a high fidelity geograph for a specific area.
322
323Follow this step by step guide on how to create a geograph from OpenStreetMap data.
324For this example, we will use some various tools to create a geograph for highways (including seconday highways) in Michigan, USA.
325
326Download an OSM PBF file using the AWS CLI:
327- Geofabrik is a good source for smaller OSM PBF files. See: https://download.geofabrik.de/
328- To keep things generalizable, you can also download the entire planet OSM PBF file using AWS. But you should consider downloading a smaller region if you are only interested in a specific area.
329    - Note: For this, you will need to install the AWS CLI.
330    - Note: The planet OSM PBF file is very large (About 100GB)
331        ```
332        aws s3 cp s3://osm-pds/planet-latest.osm.pbf .
333        ```
334- Use Osmium to filter and extract the highways from the OSM PBF file.
335    - Install osmium on macOS:
336        ```
337        brew install osmium-tool
338        ```
339    - Install osmium on Ubuntu:
340        ```
341        sudo apt-get install osmium-tool
342        ```
343- Download a Poly file for the area you are interested in. This is a polygon file that defines the area you want to extract from the OSM PBF file.
344    - For Michigan, you can download the poly file from Geofabrik:
345        ```
346        curl https://download.geofabrik.de/north-america/us/michigan.poly > michigan.poly
347        ```
348    - Google around to find an appropriate poly file for your area of interest.
349- Filter and extract as GeoJSON (EG: Michigan) substituting the poly and pbf file names as needed:
350    ```
351    osmium extract -p michigan.poly --overwrite -o michigan.osm.pbf planet-latest.osm.pbf
352    ```
353- Filter the OSM PBF file to only areas of interest and export to GeoJSON:
354    - See: https://wiki.openstreetmap.org/wiki/
355    - EG For Highways, see: https://wiki.openstreetmap.org/wiki/Key:highway
356    ```
357    osmium tags-filter michigan.osm.pbf w/highway=motorway,trunk,primary,motorway_link,trunk_link,primary_link,secondary,secondary_link,tertiary,tertiary_link -t --overwrite -o michigan_roads.osm.pbf
358    osmium export michigan_roads.osm.pbf -f geojson --overwrite -o michigan_roads.geojson
359    ```
360
361- Simplify the geojson
362    - This uses some tools in the SCGraph library as well as Mapshaper to simplify the geojson files.
363    - Mapshaper is a CLI and web tool for simplifying and editing geojson files.
364    - To install Mapshaper for CLI use, use NPM:
365        ```
366        npm install -g mapshaper
367        ```
368    - Mapshaper is particularly helpful since it repairs intersections in the lines which is crutial for geographs to work properly.
369    - Mapshaper, however, does not handle larger files very well, so it is recommended to simplify the geojson file first using the `scgraph.helpers.geojson.simplify_geojson` function first to reduce the size of the file.
370    - Make sure to tailor the parameters to your needs.
371    ```
372    python -c "from scgraph.helpers.geojson import simplify_geojson; simplify_geojson('michigan_roads.geojson', 'michigan_roads_simple.geojson', precision=4, pct_to_keep=100, min_points=3, silent=False)"
373    mapshaper michigan_roads_simple.geojson -simplify 10% -filter-fields -o force michigan_roads_simple.geojson
374    mapshaper michigan_roads_simple.geojson -snap -clean -o force michigan_roads_simple.geojson
375    ```
376- Load the newly created geojson file as a geograph:
377    - Note: The `GeoGraph.load_from_geojson` function is used to load the geojson file as a geograph.
378    - This will create a geograph that can be used to calculate shortest paths between points on the graph.
379    ```
380    from scgraph import GeoGraph
381    michigan_roads_geograph = GeoGraph.load_from_geojson('michigan_roads_simple.geojson')
382    ```
383
384## Custom Graphs and Geographs
385Modify an existing geograph: See the notebook [here](https://colab.research.google.com/github/connor-makowski/scgraph/blob/main/examples/geograph_modifications.ipynb)
386
387
388You can specify your own custom graphs for direct access to the solving algorithms. This requires the use of the low level `Graph` class
389
390```py
391from scgraph import Graph
392
393# Define an arbitrary graph
394# See the graph definitions here:
395# https://connor-makowski.github.io/scgraph/scgraph/graph.html#Graph.validate_graph
396graph = [
397    {1: 5, 2: 1},
398    {0: 5, 2: 2, 3: 1},
399    {0: 1, 1: 2, 3: 4, 4: 8},
400    {1: 1, 2: 4, 4: 3, 5: 6},
401    {2: 8, 3: 3},
402    {3: 6}
403]
404
405# Optional: Validate your graph
406Graph.validate_graph(graph=graph)
407
408# Get the shortest path between idx 0 and idx 5
409output = Graph.dijkstra_makowski(graph=graph, origin_id=0, destination_id=5)
410#=> {'path': [0, 2, 1, 3, 5], 'length': 10}
411```
412
413You can also use a slightly higher level `GeoGraph` class to work with latitude / longitude pairs
414
415```py
416from scgraph import GeoGraph
417
418# Define nodes
419# See the nodes definitions here:
420# https://connor-makowski.github.io/scgraph/scgraph/geograph.html#GeoGraph.__init__
421nodes = [
422    # London
423    [51.5074, -0.1278],
424    # Paris
425    [48.8566, 2.3522],
426    # Berlin
427    [52.5200, 13.4050],
428    # Rome
429    [41.9028, 12.4964],
430    # Madrid
431    [40.4168, -3.7038],
432    # Lisbon
433    [38.7223, -9.1393]
434]
435# Define a graph
436# See the graph definitions here:
437# https://connor-makowski.github.io/scgraph/scgraph/graph.html#Graph.validate_graph
438graph = [
439    # From London
440    {
441        # To Paris
442        1: 311,
443    },
444    # From Paris
445    {
446        # To London
447        0: 311,
448        # To Berlin
449        2: 878,
450        # To Rome
451        3: 1439,
452        # To Madrid
453        4: 1053
454    },
455    # From Berlin
456    {
457        # To Paris
458        1: 878,
459        # To Rome
460        3: 1181,
461    },
462    # From Rome
463    {
464        # To Paris
465        1: 1439,
466        # To Berlin
467        2: 1181,
468    },
469    # From Madrid
470    {
471        # To Paris
472        1: 1053,
473        # To Lisbon
474        5: 623
475    },
476    # From Lisbon
477    {
478        # To Madrid
479        4: 623
480    }
481]
482
483# Create a GeoGraph object
484my_geograph = GeoGraph(nodes=nodes, graph=graph)
485
486# Optional: Validate your graph
487my_geograph.validate_graph()
488
489# Optional: Validate your nodes
490my_geograph.validate_nodes()
491
492# Get the shortest path between two points
493# In this case, Birmingham England and Zaragoza Spain
494# Since Birmingham and Zaragoza are not in the graph,
495# the algorithm will add them into the graph.
496# See: https://connor-makowski.github.io/scgraph/scgraph/geograph.html#GeoGraph.get_shortest_path
497# Expected output would be to go from
498# Birmingham -> London -> Paris -> Madrid -> Zaragoza
499
500output = my_geograph.get_shortest_path(
501    # Birmingham England
502    origin_node = {'latitude': 52.4862, 'longitude': -1.8904},
503    # Zaragoza Spain
504    destination_node = {'latitude': 41.6488, 'longitude': -0.8891}
505)
506print(output)
507# {
508#     'length': 1799.4323,
509#     'coordinate_path': [
510#         [52.4862, -1.8904],
511#         [51.5074, -0.1278],
512#         [48.8566, 2.3522],
513#         [40.4168, -3.7038],
514#         [41.6488, -0.8891]
515#     ]
516# }
517
518```
519
520# Development
521## Running Tests, Prettifying Code, and Updating Docs
522
523Make sure Docker is installed and running on a Unix system (Linux, MacOS, WSL2).
524
525- Create a docker container and drop into a shell
526    - `./run.sh`
527- Run all tests (see ./utils/test.sh)
528    - `./run.sh test`
529- Prettify the code (see ./utils/prettify.sh)
530    - `./run.sh prettify`
531- Update the docs (see ./utils/docs.sh)
532    - `./run.sh docs`
533
534- Note: You can and should modify the `Dockerfile` to test different python versions.
535
536
537## Attributions and Thanks
538Originally inspired by [searoute](https://github.com/genthalili/searoute-py) including the use of one of their [datasets](https://github.com/genthalili/searoute-py/blob/main/searoute/data/marnet_densified_v2_old.geojson) that has been modified to work properly with this package.
539"""
540
541from .graph import Graph
542from .geograph import GeoGraph
543from .grid import GridGraph